Proviamo ad effettuare gli stessi passaggi riportati nel libro alle pagine 151 e 152, partendo però dal punto di coordinate $(200/3,sqrt(100/3))$ e verificando che esso è effettivamente la soluzione cercata, secondo il modello di Nash.



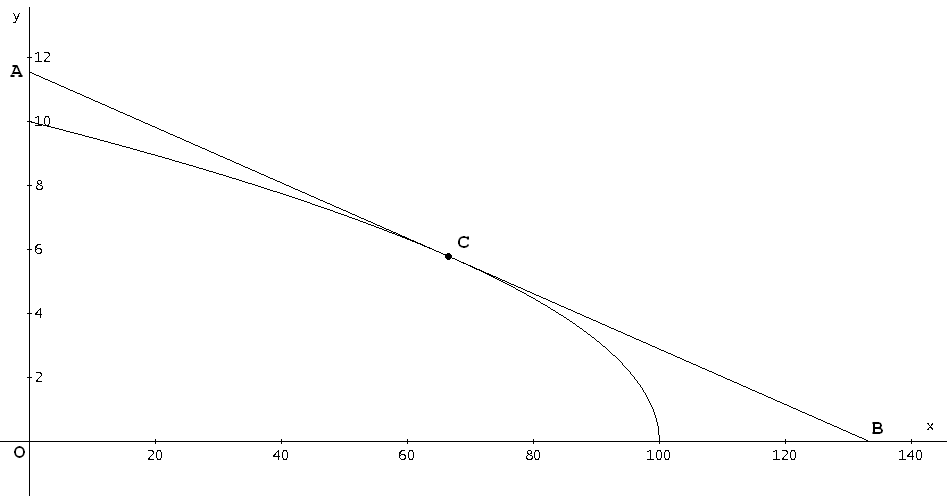
In Figura 1 il punto $(200/3,sqrt(100/3))$ è indicato con la lettera $C$. La tangente alla curva in tale punto interseca gli assi cartesiani nei punti $A(0,20/sqrt(3))$ e $B(400/3,0)$.
Il triangolo AOB contiene l'insieme di contrattazione del problema originario e quindi, per il principio di "Indipendenza dalle Alternative Irrilevanti", se la soluzione del problema avente come insieme di contrattazione il triangolo $AOB$ è contenuta nell'insieme di contrattazione di partenza, essa sarà anche soluzione del problema originario.
Tuttavia il triangolo $AOB$ non è simmetrico; per renderlo tale occorre operare una trasformazione lineare (lecita per la proprietà di covarianza) del tipo $(u_I,u_(II)) to (u'_I,u'_(II)) = (3/20 u_I, sqrt(3) u_(II))$.



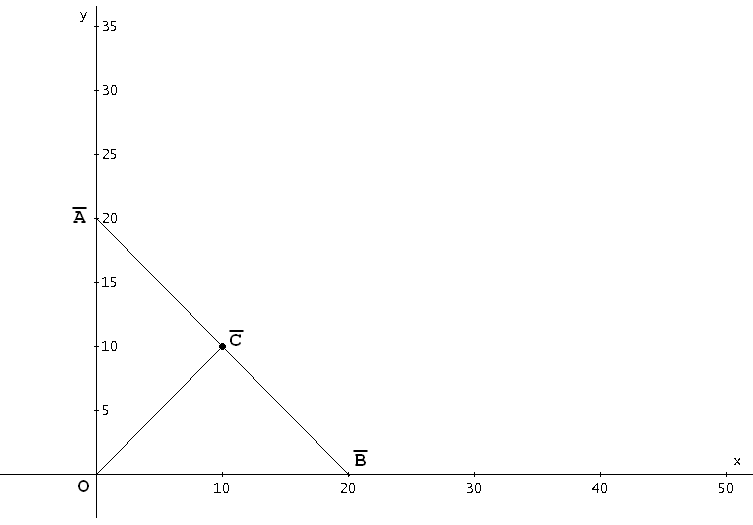
Il punto $A$ viene mappato in $bar A(0,20)$ mentre il punto $B$ viene mappato in $bar B(20,0)$ cosicché il triangolo $bar A O bar B$ risulta essere simmetrico. Sfruttando la condizione di simmetria è facile trovare la soluzione, rappresentata dal punto $bar C(10,10)$, la cui controimmagine nel triangolo di Figura 1 è proprio il punto $C$ di coordinate $(200/3,sqrt(100/3))$.

Mio commento:
No comment. Mi limito a ribadire l'importanza della condizione (riportata qui sotto in "italics") per una corretta applicazione del principio di "Indipendenza dalle Alternative Irrilevanti":
"se la soluzione del problema avente come insieme di contrattazione il triangolo $AOB$ è contenuta nell'insieme di contrattazione di partenza"